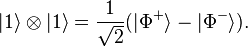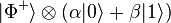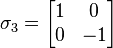This is quoted directly.
"Suppose Alice has a qubit that she wants to teleport to Bob. This qubit can be written generally as: 
Our quantum teleportation scheme requires Alice and Bob to share a maximally entangled state beforehand, for instance one of the four Bell states
 ,
, ,
, ,
, .
.
Alice takes one of the particles in the pair, and Bob keeps the other one. The subscripts A and B in the entangled state refer to Alice's or Bob's particle. We will assume that Alice and Bob share the entangled state 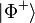 .
.
So, Alice has two particles (C, the one she wants to teleport, and A, one of the entangled pair), and Bob has one particle, B. In the total system, the state of these three particles is given by
Alice will then make a partial measurement in the Bell basis on the two qubits in her possession. To make the result of her measurement clear, we will rewrite the two qubits of Alice in the Bell basis via the following general identities (these can be easily verified):
and
The three particle state shown above thus becomes the following four-term superposition:
Notice all we have done so far is a change of basis on Alice's part of the system. No operation has been performed and the three particles are still in the same state. The actual teleportation starts when Alice measures her two qubits in the Bell basis. Given the above expression, evidently the results of her (local) measurement is that the three-particle state would collapse to one of the following four states (with equal probability of obtaining each):
Alice's two particles are now entangled to each other, in one of the four Bell states. The entanglement originally shared between Alice's and Bob's is now broken. Bob's particle takes on one of the four superposition states shown above. Note how Bob's qubit is now in a state that resembles the state to be teleported. The four possible states for Bob's qubit are unitary images of the state to be teleported.
The crucial step, the local measurement done by Alice on the Bell basis, is done. It is clear how to proceed further. Alice now has complete knowledge of the state of the three particles; the result of her Bell measurement tells her which of the four states the system is in. She simply has to send her results to Bob through a classical channel. Two classical bits can communicate which of the four results she obtained.
After Bob receives the message from Alice, he will know which of the four states his particle is in. Using this information, he performs a unitary operation on his particle to transform it to the desired state  :
:
- If Alice indicates her result is
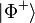 , Bob knows his qubit is already in the desired state and does nothing. This amounts to the trivial unitary operation, the identity operator.
, Bob knows his qubit is already in the desired state and does nothing. This amounts to the trivial unitary operation, the identity operator.
- If the message indicates
 , Bob would send his qubit through the unitary gate given by the Pauli matrix
, Bob would send his qubit through the unitary gate given by the Pauli matrix
to recover the state.
- If Alice's message corresponds to
 , Bob applies the gate
, Bob applies the gate
to his qubit.
- Finally, for the remaining case, the appropriate gate is given by
Teleportation is therefore achieved.
Experimentally, the projective measurement done by Alice may be achieved via a series of laser pulses directed at the two particles."
Hey, thanks wikpedia. I'm glad to know that two random computer engineers know so much about quantum computing that if necessary Alice and Bob could stay in touch via quantum teleportation.Someone may think "oh, but Ryan, it's so much easier to understand quantum computing this way!" Yeah, well. I always thought situations were more for, say, "Alice has five apples. She gives three to Bob. How many apples does Alice have now?"